|
This is the 3rd lesson in the Polyrhythm series.
Lesson One: An Introduction to Polyrhythms Lesson Two: How to Play Polymeters
In this lesson we will look at a simple way of spacing out polyrhythms and how to count them.
There are multiple ways to figure out how to play, understand, and count a polyrhythm, but my goal is to show you how to do this in a simple and effective manner. Let's begin with a 3:2 polyrhythm. How do you evenly space the notes, or beats, on top of 2 different evenly spaced notes, or beats? One way I've seen this done, is to write out groups of numbers in rows. For the 3:2 polyrhythm you can write out two rows of numbers that go 1 2 3.
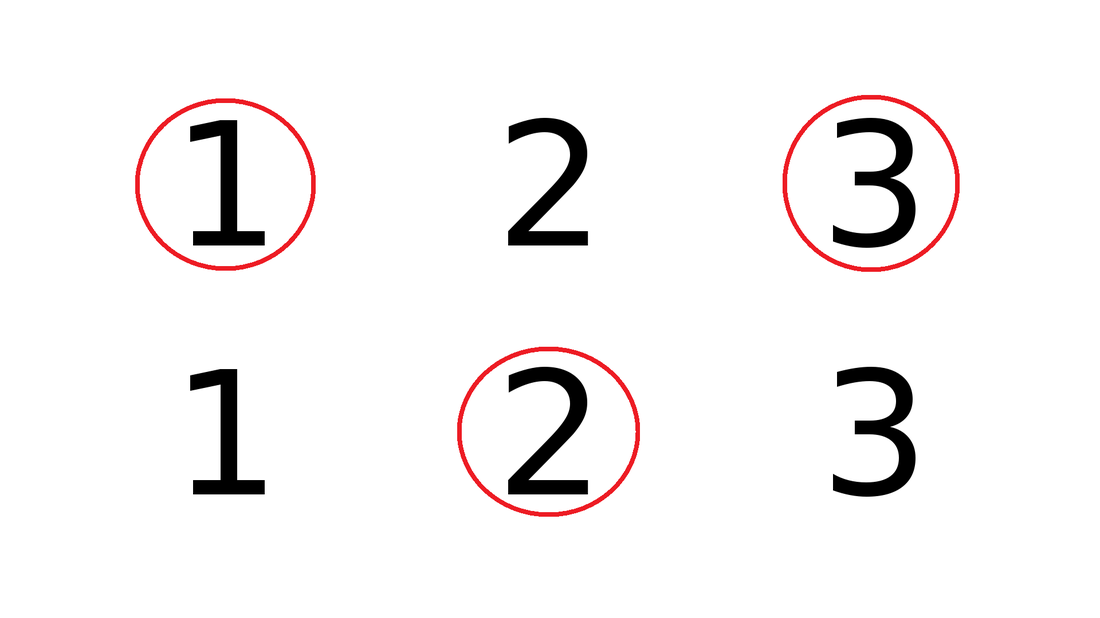
Then, you circle the first number for every group of two numbers.
Each row represents one full beat. There are two beats shown in this example. Each beat is divided into 3 even parts. The circled numbers represent the parts of the beat where you play 3 evenly spaced notes. The 1 in both beats represent where you play 2 evenly spaced notes.
How this sounds, and other examples in this lesson will be demonstrated in the video found at the end of this entry.
This same method can be applied to any polyrhythm. The 2nd number in the polyrhythm is how many rows of numbers you will write out. The 1st number in the polyrhythm is how many numbers you will write in each row. The 2nd number also tells you how many groups of numbers there need to be so you know which numbers to circle.
A 4:3 polyrhythm will get 3 rows, and each row will have 1 2 3 4. You will circle the first number for each grouping of 3 numbers.
A 5:4 polyrhythm will get 4 rows, and each row will have 1 2 3 4 5. You will circle the first number for each grouping of 4 numbers.
Now, here's the problem I have with that method. Typically, you do not count out the parts of a measure, or beats with just numbers. For example, a piece of music playing straight 16th notes for four beats is typically counted out as 1ena2ena3ena4ena. Not 1234123412341234.
Counting out 1ena2ena3ena4ena helps you keep track of what beat you are on. Counting 1234123412341234 does not.
Let's talk about how I prefer to figure out and count polyrhythms. Let's take a look at the 3:2 polyrhythm again. The number 2, in the 3:2 polyrhythm, is our main number. We are working with 2 beats. The number 3, in the 3:2 polyrhythm, is our secondary number. The goal here is to space 3 notes over 2 notes. So, what has to happen in order to use a more typical method of counting music is the beat must be divided into 3 parts. And what happens when you divide a beat into 3 even parts? You get a triplet! Now we can view the beats like this:
1na2na
Just like before, the number 2 in our 3:2 polyrhythm tells us where in the beat we play the 3 evenly spaced notes. If you underline the first part of every two parts in the beats, you will know how to space the 3 notes over the 2 beats while using a more common method of counting rhythm.
1na2na
How about 4:3? 4:3 tells you we have 3 beats as our base. Each beat is divided into 4 parts. Counting 16th notes will get the job done here.
1ena2ena3ena
Now, underline the first part of every 3 parts in the beat.
1ena2ena3ena
What about the 5:4 polyrhythm? This one gets a little tricky. You need to divide each of the 4 beats into 5 equal parts. Dividing a beat into 5 parts is not a common thing to do. However, that does not mean it is impossible. My recommendation for counting out 5 equal parts per beat, with 4 beats total, is this:
1enae2enae3enae4enae
This allows us to keep track of what beat we are on, and I feel it's fairly simple to say.
Just like the previous two examples, portions of this rhythm, or parts of the beat, need to be underlined so we can see where in the beat we are going to play. Remember, the 2nd number in the polyrhythm ratio tells you how to group the parts of the beat. Because we are working with a 5:4 polyrhythm we will underline the first part of every 4 parts. It will look like this:
1enae2enae3enae4enae
Developing the ability to comfortably count these rhythms can take a while. Like anything else in music, taking small steps in learning something difficult can and will help you help you learn difficult things in the shortest amount of time possible.
Watch the following video on how to approach adding small pieces to learn a complex rhythm.
Would you like to be a part of getting more lessons like this made? CLICK HERE to see how you can help!
0 Comments
Leave a Reply. |
Available Instruction Courses
|
- Metal and Rock Guitar Lessons
- Reach Your Fastest Speeds
-
Menu
- Skype Lessons
- Sign Up for Skype Guitar Lessons
- Video Correspondence Lessons
- Sign Up for Video Correspondence Lessons
- FREE Lessons for a WEEK >
- Free Tabs
- Get TWO FREE eBooks
- Rates
- Instruction Courses >
- Video Feedback Lessons
- Contact
- Blog (LOTS of Free Lessons)
- Student Testimonies
- Backing Tracks
- Store
IN DEPTH
|
|

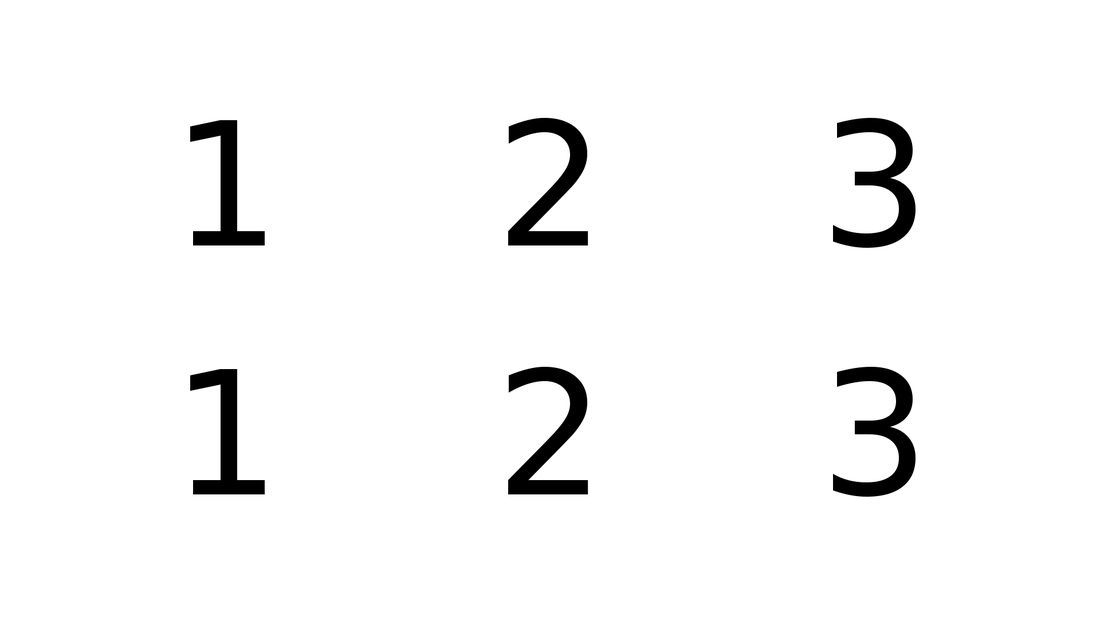







 RSS Feed
RSS Feed